特征空间映射

1. 问题

• 简单的0,1分类 – 即标签$y =$ {$0,1$}
• 特征值：$x = [x_1, x_2]$二维

数据离散点如图：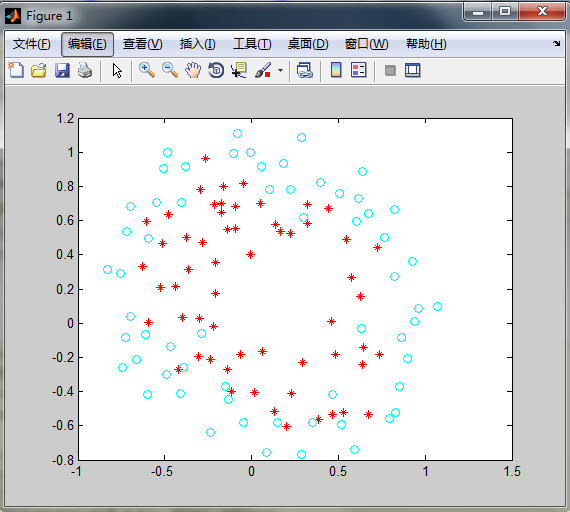

2.解答

• 数据是二维的，因此如果利用Logistics Regression 的到的$\theta$只有三个数，所以分类超平面是二维坐标下的直线
• 由数据分布图可以知道分类超平面应该是一个二次曲线，所以这里利用多项式核函数：$K = (<x_1, x_2> + R)^d$，令R= 1， d = 2.可以得出二维数据映射到五维时，二次曲线成为五维空间中的直线，因此我们将二维数据$x = [x_1, x_2]$ 扩展到五维$x = [x_1, x_1^2, x_2, x_2^2, x_1x_2]$
• 因此超平面表达式如下：
  $\theta_1 + \theta_2*x_1 + \theta_3*x_1^2 + \theta_4*x_2 + \theta_5*x_2^2 + \theta_6*x_1x_2 = 0$
• $\theta$和$J$的计算方式依然不变，这里采用fminunc函数计算最优解

3.效果如下

　　　最后结果：
　　

theta =    5.1555    3.2317  -11.9929    4.1505  -11.7849   -7.4954>> costcost =    0.3481

图形如下：

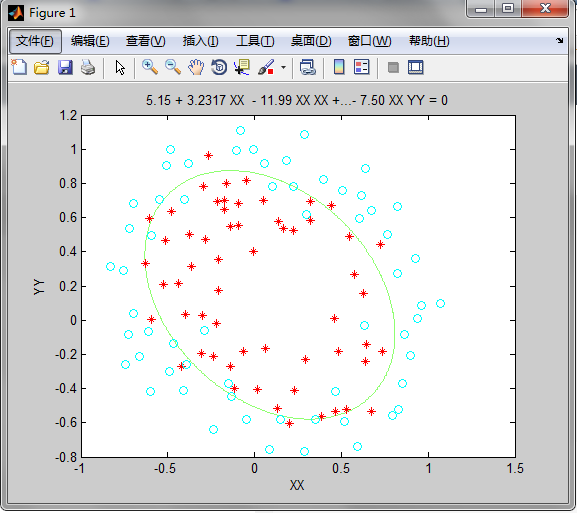
代码

1. Logistics_Regression

%%  part0： 准备data = load('ex2data2.txt');x = data(:,[1,2]);y = data(:,3);pos = find(y==1);neg = find(y==0);x1 = x(:,1);x2 = x(:,2);plot(x(pos,1),x(pos,2),'r*',x(neg,1),x(neg,2),'co');m = size(y,1);X = zeros(m,6);X(:,1) = ones(m,1);X(:,2) = x(:,1);X(:,3) = x(:,1).*x(:,1);X(:,4) = x(:,2);X(:,5) = x(:,2).*x(:,2);X(:,6) = x(:,1).*x(:,2);pause;%% part1: GradientDecent and compute cost of J[m,n] = size(X);theta = zeros(6,1);options = optimset('GradObj', 'on', 'MaxIter', 400);%  Run fminunc to obtain the optimal theta%  This function will return theta and the cost [theta, cost] = ...    fminunc(@(t)(computeCost(X,y,t)), theta, options);display(theta);ezplot('5.15 + 3.2317*XX  - 11.99*XX*XX + 4.15*YY  - 11.78*YY*YY  - 7.50*XX*YY',[-1.0,1.5,-0.8,1.2]);hold onplot(x(pos,1),x(pos,2),'r*',x(neg,1),x(neg,2),'co');pause;

2.computeCost

function [J,grad] = computeCost(x, y, theta)%% compute cost: Jm = size(x,1);grad = zeros(size(theta));hx = sigmoid(x * theta);   J = (1.0/m) * sum(-y .* log(hx) - (1.0 - y) .* log(1.0 - hx));   grad = (1.0/m) .* x' * (hx - y);end

3.sigmoid

function g = sigmoid(z)%% SIGMOID Compute sigmoid functoong = zeros(size(z));g = 1.0 ./ (1.0 + exp(-z));end