一. 数据描述
来源:数据集合(http://download.csdn.net/detail/huangxia73/7059709)
描述:电信数据,有多个属性,用来预测客户流失。
载入数据如下:
> call_consumer<-read.table(file="d:/LabData/RData/churn.txt",header=TRUE,sep=",")Warning message:In read.table(file = "d:/LabData/RData/churn.txt", header = TRUE, : incomplete final line found by readTableHeader on 'd:/LabData/RData/churn.txt'> edit(call_consumer)数据概况如下:

二 .解读逻辑回归模型
分三种:
(1)一个两分预测变量的模型
(2)多分预测变量
(3)连续的预测变量
2.1 两分预测变量模型
假定唯一的预测变量是语音邮箱套餐(Intl.plan),这是一个表示是否为套餐会员的标记变量。下表显示了语音邮箱套餐会员流失情况。
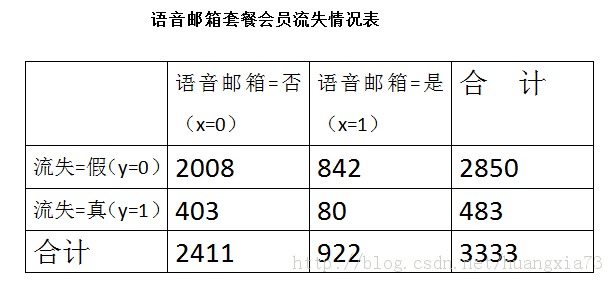
似然函数可以表示为:
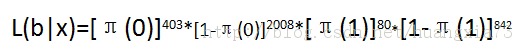
.使用语音邮箱套餐的客户流失的发生比=π(1)/[1-π(1)]=80/842=0.095
.没有使用语音邮箱套餐的客户流失的发生比=π(0)/[1-π(0)]=403/2008=0.2007
故:
OR=0.095/0.2007=0.47
也即 使用语音邮箱套餐的客户与没有使用语音邮箱套餐的客户相比,流失概率只有47%
下图显示了语音套餐会员流失的逻辑回归结果

可以得到b0=-1.60596和b1=-0.747795.所以用于语音邮箱套餐(x=1)的客户或者没有语音套餐(x=0)的客户流失的估计值为:

(1)对于一个拥有此套餐的客户,估计他的流失概率为:上式子中x=1得:π(1)=0.0868(也可以直接计算 P(流失|语音邮箱计划)=80/922=0.0868),这一概率比数据集中给出的客户流失的总比例14.5%要小,说明开通语音邮箱套餐有利于减少客户流失。
(2)对于一个没有拥有此套餐的客户,估计他的流失概率为:上式子中x=0得:π(0)=0.16715(也可以直接计算 P(流失|语音邮箱计划)=403/2411=0.16715),这一概率比数据集中给出的客户流失的总比例14.5%要高,说明没有开通语音邮箱套餐对于客户流失不大。
进一步地,可以利用Wald检验法检验语音邮箱套餐参数的显著性。这里,b1=-0.747795,SE(b1)=0.129101得:
Zwald=-0.747795/0.129101=-5.79
P值为P(|Z|>-5.79)-->=0,表明显著性很强。
2.2 多分预测变量模型
假定将客户服务电话数(customers services calls)看做一个新的变量-CSC,分类如下:
(1)0个或1个客户服务电话:CSC=低
(2)2个或3个客户服务电话:CSC=中
(3)4个以上客户服务电话:CSC=高
此时,分析人员需要用指示变量(虚拟变量)和参考单元编码法来给数据集编码,假定选择“CSC=低”作为参考单元,则可把指示变量值分配给另外两个变量。使用指示变量之后:
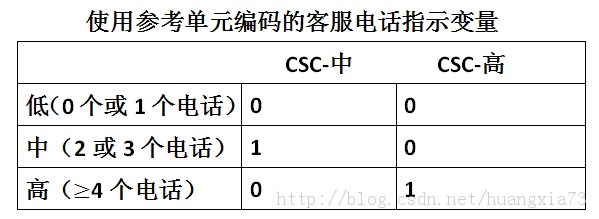
使用CSC展示客户流失情况列表汇总如下:
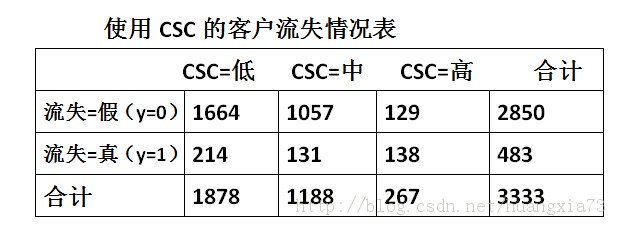
此时再对数据进行逻辑回归分析,得到的结果如下(注意:没有CSC-低):
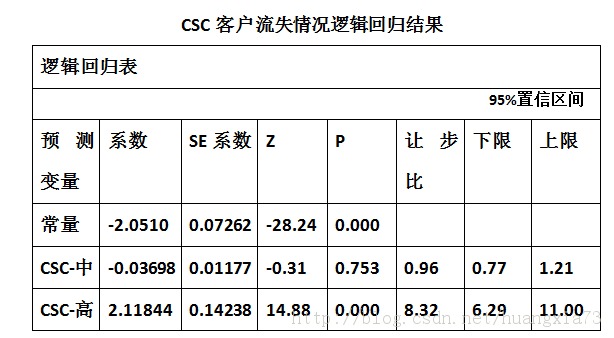
.对于CSC-中:OR^=e^b1=e^-0.03698=0.96
.对于CSC-高:OR^=e^b2=e^2.11844=8.32
这里,b0=-2.501,b1=-0.03698,b2=2.11844,所以客户流失概率的估计量为:

(1)对于那些很少拨打客服电话的客户:
g(x)=-2.501-0.036989(0)+2.11844(0)=-2.051
故概率为:π(x)=e^-2.051/1+e^-2.051=0.114
此概率比全部数据样本集中客户流失的概率14.5%要小。这表明这一类客户的流失率一定程度上比总体客 户的流失率要小
(2)对于拨打客服电话处于中等水平的客户,同上,此时
g(x)=-2.501-0.036989(1)+2.11844(0)=-2.088
(3)对于经常拨打客服电话的客户,同上,此时:
g(x)=-2.501-0.036989(0)+2.11844(1)=0.06744
Wald检验
(1)对于CSC-中 的参数进行Wald检验,b1=-0.036989,SE(b1)=0.117701
故而,Zwald=-0.036989/0.117701=-0.31426
此时,P值P(|Z|>0.31426)=0.753,不显著,所以没有证据表明CSC-中与CSC -低 的差异能有效预测客户流失。
(2)对于CSC-高 的参数进行Wald检验,b1=2.11844,SE(b1)=0.142380
故而,Zwald=2.11844/0.142380=14.88
此时,P值P(|Z|>14.88)=0.000,显著,表明CSC-高与CSC-低的差异能有效预测客户流失。
【所以,对于多分预测变量模型,关键是指示变量和参照单元编码】2.3 解读连续预测变量模型
假定我们考虑以客户日使用分钟数作为预测变量,则相应的逻辑回归分析结果如下:
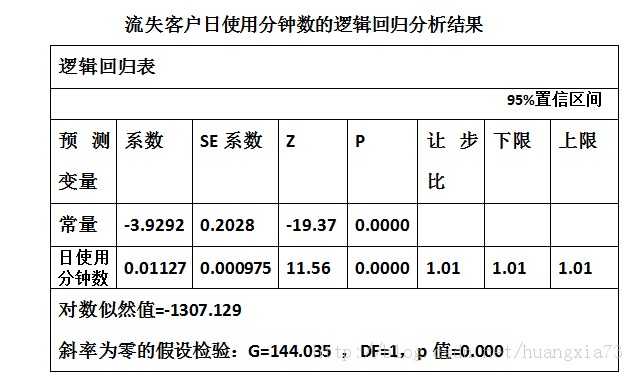
因此对于一个给定日使用分钟数的顾客,流失概率:

(1)对于一个日使用分钟数为100的顾客流失的概率估计为:
g(x)=-3.9292+0.0112717(100)=-2.80212
概率π(100)=0.0572,比数据集中总比例14.5%要小,表明低的日使用分钟数会在一定程 度上防止顾客流失
(2)对于一个日使用分钟数为300的顾客流失的概率估计为:
g(x)=-3.9292+0.0112717(300)=-0.054778
概率π(300)=0.3664,比数据集中总比例14.5%要大,表明日使用分钟数越多顾客流失越 多
“日使用分钟数”,这一实例的偏差G为:
G=偏差(没有预测变量的模型)-偏差(有预测变量的模型)
=-2ln[没有预测变量的似然值/有预测变 量的似然值]
=2{-1307.129-[483ln(483)+2850ln(2850)-3333ln(333 3)]}
=144.035
对G进行卡方检验,p值为P(x^2)>G观测值=P(x^2)>144.035=0.000,因此强有力的证据表明日使用分钟数有助于预测顾客的流失情况。
对“日使用分钟数”进行Wald检验,可以得到同样的结论。
3. 多元逻辑回归
多元逻辑回归与简单逻辑回归十分相似,需要注意的是选择恰当的预测变量,其方法主要有
(1)针对单个变量的挑选: wald检验某个变量是否有助于预测
(1)针对单个变量的挑选: wald检验某个变量是否有助于预测
(2)针对多个变量总体挑选:总体显著性G
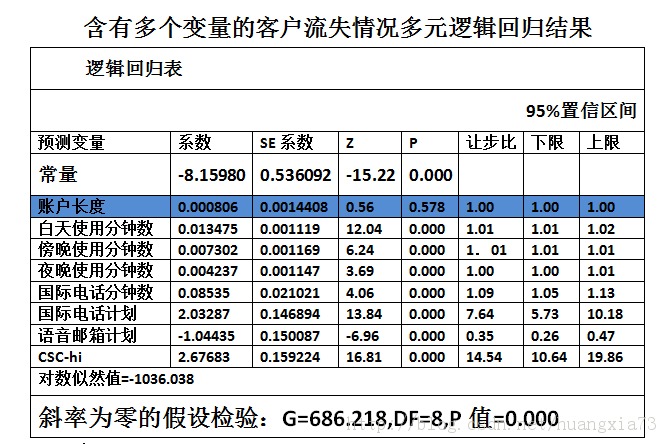
下图一个简单示例:
表1

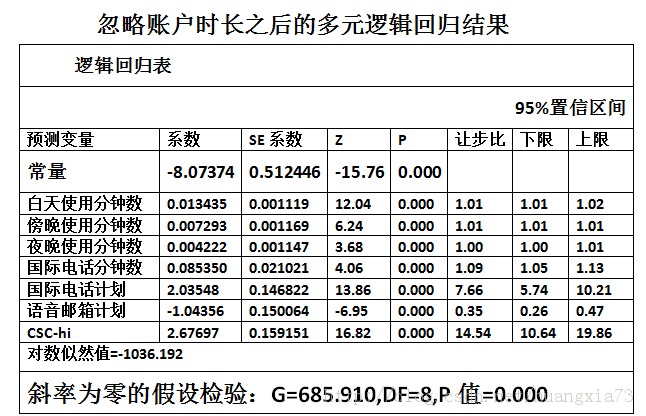
表2

由上面两幅图可以看出,其中的“账户时长”变量其Wald检验的P值没有拒绝零假设检验,因而需要从全体预测变量中剔除。最后的G偏差,卡方检验虽然两幅图中都能表明,多元预测变量能显著预测结果(G检验的P值=0),但是剔除账户长度后更好。
4. 逻辑回归中引入高阶项
如果逻辑回归转换函数在连续变量中不是线性的,让步比的估计和置信区间的应用可能会有问题。原因在与估计的让步比在预测变量取值域上是一个常数。例如,不论是第23分钟还是第323分钟,日使用分钟数每增加1个单位,让步比都是1.01.这种让步比为常数的假设并不总是成立。
此时,分析人员需要做一些非线性的调整,如使用指示变量(见多分预测变量模型)和高阶项(如:x^2,x^3..)。
高阶项的引入可以作为惩罚函数,减少该变量不正常的分布。使用高阶项(和起始变量一起运用)的优势在于,高阶项可以是连续的并且可以提供更严格的估计。