1. ID3 算法

ID3 算法是一种典型的决策树（decision tree）算法，C4.5, CART都是在其基础上发展而来。决策树的叶子节点表示类标号，非叶子节点作为属性测试条件。从树的根节点开始，将测试条件用于检验记录，根据测试结果选择恰当的分支；直至到达叶子节点，叶子节点的类标号即为该记录的类别。

ID3采用信息增益（information gain）作为分裂属性的度量，最佳分裂等价于求解最大的信息增益。

信息增益=parent节点熵 - 带权的子女节点的熵

ID3算法流程如下：

1.如果节点的所有类标号相同，停止分裂；

2.如果没有feature可供分裂，根据多数表决确定该节点的类标号，并停止分裂；

3.选择最佳分裂的feature，根据选择feature的值逐一进行分裂；递归地构造决策树。

源代码（从[1]中拿过来）：

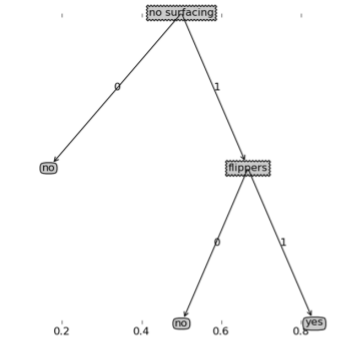
from math import logimport operatorimport matplotlib.pyplot as pltdef calcEntropy(dataSet):    """calculate the shannon entropy"""    numEntries=len(dataSet)    labelCounts={}    for entry in dataSet:        entry_label=entry[-1]        if entry_label not in labelCounts:            labelCounts[entry_label]=0        labelCounts[entry_label]+=1    entropy=0.0    for key in labelCounts:        prob=float(labelCounts[key])/numEntries        entropy-=prob*log(prob,2)    return entropydef createDataSet():    dataSet = [[1, 1, 'yes'],            [1, 1, 'yes'],            [1, 0, 'no'],            [0, 1, 'no'],            [0, 1, 'no']]    labels = ['no surfacing','flippers']    return dataSet, labelsdef splitDataSet(dataSet,axis,pivot):    """split dataset on feature"""    retDataSet=[]    for entry in dataSet:        if entry[axis]==pivot:            reduced_entry=entry[:axis]            reduced_entry.extend(entry[axis+1:])            retDataSet.append(reduced_entry)    return retDataSetdef bestFeatureToSplit(dataSet):    """chooose the best feature to split """    numFeatures=len(dataSet[0])-1    baseEntropy=calcEntropy(dataSet)    bestInfoGain=0.0; bestFeature=-1    for axis in range(numFeatures):        #create unique list of class labels        featureList=[entry[axis] for entry in dataSet]        uniqueFeaList=set(featureList)        newEntropy=0.0        for value in uniqueFeaList:            subDataSet=splitDataSet(dataSet,axis,value)            prob=float(len(subDataSet))/len(dataSet)            newEntropy+=prob*calcEntropy(subDataSet)        infoGain=baseEntropy-newEntropy        #find the best infomation gain        if infoGain>bestInfoGain:            bestInfoGain=infoGain            bestFeature=axis    return bestFeaturedef majorityVote(classList):    """take a majority vote"""    classCount={}    for vote in classList:        if vote not in classCount.keys():            classCount[vote]=0        classCount+=1    sortedClassCount=sorted(classCount.iteritems(),            key=operator.itemgetter(1),reverse=True)    return sortedClassCount[0][0]def createTree(dataSet,labels):    classList=[entry[-1] for entry in dataSet]    #stop when all classes are equal    if classList.count(classList[0])==len(classList):        return classList[0]    #when no more features, return majority vote    if len(dataSet[0])==1:        return majorityVote(classList)       bestFeature=bestFeatureToSplit(dataSet)    bestFeatLabel=labels[bestFeature]    myTree={bestFeatLabel:{}}    del(labels[bestFeature])    subLabels=labels[:]    featureList=[entry[bestFeature] for entry in dataSet]    uniqueFeaList=set(featureList)    #split dataset according to the values of the best feature    for value in uniqueFeaList:        subDataSet=splitDataSet(dataSet,bestFeature,value)        myTree[bestFeatLabel][value]=createTree(subDataSet,subLabels)    return myTree

2. Referrence

[1] Peter Harrington, machine learning in action.