hdu2196-Computer（树形DP习题2）

Description

A school bought the first computer some time ago(so this computer's id is 1). During the recent years the school bought N-1 new computers. Each new computer was connected to one of settled earlier. Managers of school are anxious about slow functioning of the net and want to know the maximum distance Si for which i-th computer needs to send signal (i.e. length of cable to the most distant computer). You need to provide this information. 


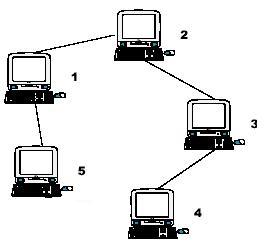
Hint: the example input is corresponding to this graph. And from the graph, you can see that the computer 4 is farthest one from 1, so S1 = 3. Computer 4 and 5 are the farthest ones from 2, so S2 = 2. Computer 5 is the farthest one from 3, so S3 = 3. we also get S4 = 4, S5 = 4.

 

Input

Input file contains multiple test cases.In each case there is natural number N (N<=10000) in the first line, followed by (N-1) lines with descriptions of computers. i-th line contains two natural numbers - number of computer, to which i-th computer is connected and length of cable used for connection. Total length of cable does not exceed 10^9. Numbers in lines of input are separated by a space.

 

Output

For each case output N lines. i-th line must contain number Si for i-th computer (1<=i<=N).

 

Sample Input

 51 12 13 11 1 

 

Sample Output

 32344 

给出电脑之间连接的关系，和相互之间的长度，求每台电脑到最远的一个的距离是多少。

对于一个点i来说，i能到的最远距离可能有两种情况：

1.由i走向i的子节点存在最远长度。（向下）

2.由i走向i的父节点存在最远长度。 （向上）

dp[i][0]记录节点i向下的最长距离，belong[i][0]记录向下最长路径经过的i的子节点。

dp[i][0]记录节点i向下的第二长距离，belong[i][0]记录向下第二长路径经过的i的子节点。

flag[i] = 0代表i的父节点的最长路径不经过i， = 1 代表i的父节点的最长路径经过i

状态转移方程：先由dfs，找出所有点向下的距离，然后由上向下层次遍历

设 i是j的父节点

如果节点j的flag[j] = 0 ,那么它的最远距离应该是dp[j][0] 和 i的最远距离+i到j的距离 中的最大值。

如果节点j的flag[j] = 1 ,那么它的最远距离应该是 dp[j][0] 和 i的非包含j的路径的距离+i到j的距离 中的最大值。

#include <cstdio>#include <cstring>#include <algorithm>#include <queue>using namespace std ;struct node{    int u , v , w ;    int next ;}edge[11000];int head[11000] , cnt ;int dp[11000][2] , flag[11000] , belong[11000][2];queue <int> que ;void add(int u,int v,int w){    edge[cnt].u = u ; edge[cnt].v = v ;    edge[cnt].w = w ;    edge[cnt].next = head[u] ;    head[u] = cnt++ ;}void dfs(int u){    if( head[u] == -1 )        return ;    int i , v , k1 , k2 ;    for( i = head[u] ; i != -1 ; i = edge[i].next )    {        v = edge[i].v ;        dfs(v) ;        if( dp[v][0]+edge[i].w > dp[u][0] )        {            dp[u][1] = dp[u][0] ; belong[u][1] = belong[u][0] ;            dp[u][0] = dp[v][0]+edge[i].w ; belong[u][0] = v ;        }        else if( dp[v][0]+edge[i].w > dp[u][1] )        {            dp[u][1] = dp[v][0]+edge[i].w ; belong[u][1] = v ;        }    }}int main(){    int n , u , v , w ;    int i ;    while( scanf("%d", &n) != EOF )    {        memset(flag,0,sizeof(flag)) ;        memset(dp,0,sizeof(dp)) ;        memset(head,-1,sizeof(head)) ;        memset(belong,0,sizeof(belong)) ;        cnt = 0 ;        add(0,1,0) ;        for(i = 2 ; i <= n ; i++)        {            scanf("%d %d", &u, &w) ;            add(u,i,w) ;        }        dfs(1) ;        while( !que.empty() ) que.pop() ;        que.push(0) ;        while( !que.empty() )        {            u = que.front() ;            que.pop() ;            for(i = head[u] ; i != -1 ; i = edge[i].next)            {                v = edge[i].v ;                if( flag[v] )                {                    if( dp[v][0] + edge[i].w == dp[u][0] )                    {                        if( dp[u][1]+edge[i].w > dp[v][0] )                        {                            flag[ belong[v][0] ] = 1;                            dp[v][1] = dp[v][0] ;                            dp[v][0] = dp[u][1]+edge[i].w ;                        }                        else if( dp[u][1] + edge[i].w > dp[v][1] )                        {                            flag[ belong[v][0] ] = 1 ;                            dp[v][1] = dp[u][1] + edge[i].w ;                        }                        else                        {                            flag[ belong[v][0] ] = 1 ;                            flag[ belong[v][1] ] = 1 ;                        }                    }                    else                    {                        if( dp[u][0]+edge[i].w > dp[v][0] )                        {                            flag[ belong[v][0] ] = 1;                            dp[v][1] = dp[v][0] ;                            dp[v][0] = dp[u][0]+edge[i].w ;                        }                        else if( dp[u][0] + edge[i].w > dp[v][1] )                        {                            flag[ belong[v][0] ] = 1 ;                            dp[v][1] = dp[u][0] + edge[i].w ;                        }                        else                        {                            flag[ belong[v][0] ] = 1 ;                            flag[ belong[v][1] ] = 1 ;                        }                    }                }                else                {                    if( dp[u][0]+edge[i].w > dp[v][0] )                    {                        flag[ belong[v][0] ] = 1;                        dp[v][1] = dp[v][0] ;                        dp[v][0] = dp[u][0]+edge[i].w ;                    }                    else if( dp[u][0] + edge[i].w > dp[v][1] )                    {                        flag[ belong[v][0] ] = 1 ;                        dp[v][1] = dp[u][0] + edge[i].w ;                    }                    else                    {                        flag[ belong[v][0] ] = 1 ;                        flag[ belong[v][1] ] = 1 ;                    }                }                que.push(v) ;            }        }        for(i = 1 ; i <= n ; i++)            printf("%d\n", dp[i][0]) ;    }    return 0;}