帮忙瞅个代码

帮忙看个代码
    问题及算法大概是这样的：将正整数n表示成一系列正整数之和：n=n1+n2+..........nk，其中n1>=n2>=........nk；k>=1。
求n的不同划分个数
例如6有如下的划分个数：
6；
5+1；
4+2；4+1+1；
3+3；3+2+1；3+1+1+1；
2+2+2；2+2+1+1；2+1+1+1+1；
1+1+1+1+1+1；

分析：将最大加数不大于m的划分个数记作p(n，m)。可建立如下关系
       1 、p(n，1) = 1;
       2 、m>=n    p(n，m) =p(n，n)；
       3 、p(n，n) = p(n，n-1)+1；
       4 、p(n，m) = p(n，m-1)+p(n-m，m)；n>m   

我写的代码及运行结果：


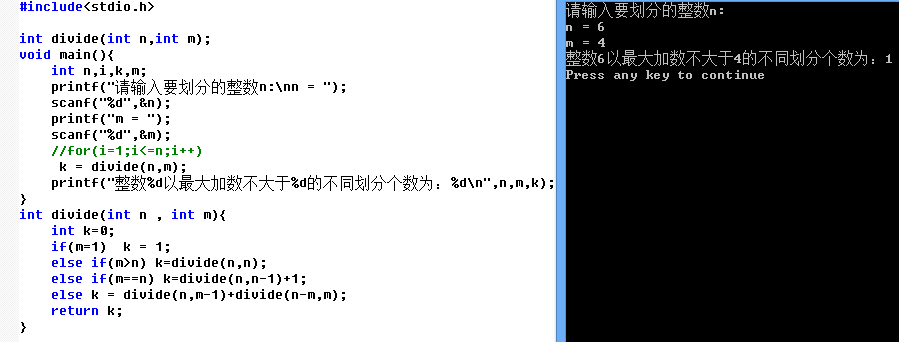
不知道哪里错了，麻烦帮我看下。
------解决方案--------------------------------------------------------

if(m == 1)

------解决方案--------------------------------------------------------
单步调试和设断点调试是程序员必须掌握的技能之一。