希尔排序(Shell Sort) |
排序思想:
先取一个小于n的整数d1作为第一个增量,把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序;然后,取第二个增量d2<d1重复上述的分组和排序,直至所取的增量 dt=1(dt<dt-1…<d2<d1),即所有记录放在同一组中进行直接插入排序为止。
复杂度:O(n3/2)。
稳定性:不稳定。

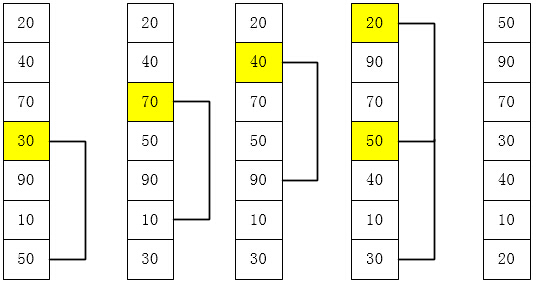


代码实例:
int[] list = { 50, 10, 90, 30, 70, 40, 20 };int len = list.Length;int temp, j;while (len > 1){ len = len / 2; for (int i = len; i < list.Length; i++) { if (list[i] < list[i - len]) { temp = list[i]; for (j = i - len; j >= 0 && temp < list[j]; j = j - len) { list[j + len] = list[j]; } list[j + len] = temp; } }}Console.WriteLine("希尔排序的结果:{0}",string.Join(",", list));
堆排序(Heap Sort ) |
排序思想:指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。
堆是具有下列性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。
复杂度:O(nlogn)。
稳定性:不稳定。

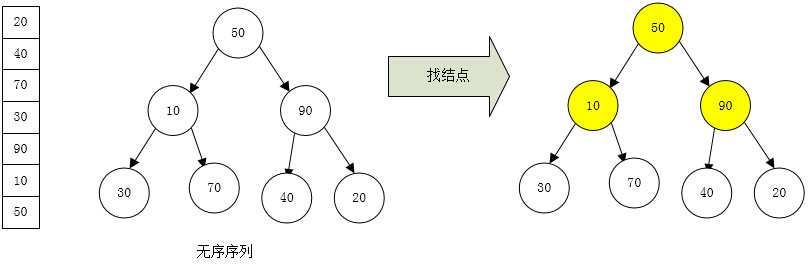


堆排序只用做以下二点:
1:从无序序列中构建起大顶堆。
2:交换大顶堆中顶节点和后结点(n)位置,重新调整剩余元素,构建一个新的大顶堆。依次循环....
代码实例:
static void Main(string[] args){ int[] list = { 50, 10, 90, 30, 70, 40, 20 }; for (int i = list.Length / 2 - 1; i >= 0; i--) /* 构建大顶堆[list.Length / 2 - 1:无序数组中结点数]*/ { HeapAdjust(list, i, list.Length); } int temp; for (int i = list.Length - 1; i > 0; i--) /* 替换大顶堆的位置,然后重新构建大顶堆。*/ { temp = list[0]; /* 替换大顶堆中最大值list[0]和最小值之前的位置list[i]*/ list[0] = list[i]; list[i] = temp; HeapAdjust(list, 0, i); /* 重新构建大顶堆*/ } Console.WriteLine("堆排序的结果:{0}", string.Join(",", list));}/// <summary>/// 构建大顶堆/// </summary>/// <param name="list">排序集合</param>/// <param name="NodeIndex">父结点</param>/// <param name="len">大顶堆长度</param>static void HeapAdjust(int[] list, int NodeIndex, int len){ int temp = list[NodeIndex]; /*二叉树节点值*/ for (int i = NodeIndex * 2 + 1; i < len; i = NodeIndex * 2 + 1) /*循环二叉树节点下左右孩子[NodeIndex*2+1找到结点下的左右孩子]*/ { if (i + 1 < len && list[i] < list[i + 1]) /*i+1:是否存在左右两个孩子,list[i]<list[i+1]:默认左孩子大于右孩子*/ { i++; /*左孩子小于右孩子直接i++ ,list[i]为右孩子值*/ } if (temp >= list[i]) /*节点大于等于(左/右)孩子直接退出不替换节点值*/ { break; } list[NodeIndex] = list[i]; /*替换节点和(左/右)孩子之间的值,保持结点大于左右孩子*/ NodeIndex = i; /*重新设置结点值,循环查询*/ } list[NodeIndex] = temp; /*替换(左/右)孩子和结点之间的值*/}
归并排序(Merge sort) |
排序思想:“归并”一词的中文含义就是合并、并入的意思,而在数据结构中的定义是将两个或两个以上的有序表组合成一个新的有序表。
归并排序(Merging Sort)就是利用归并的思想实现的排序方法。它的原理是假设初始序列含有n个记录,则可以看成是n个有序的子序列,每个子序列的长度为1,然后两两归并,得到⌈n/2⌉(⌈x⌉表示不小于x的最小整数)个长度为2或1的有序子序列;再两两归并,……,如此重复,直至得到一个长度为n的有序序列为止,这种排序方法称为2路归并排序。
复杂度:O(nlogn) 。
稳定性:稳定。
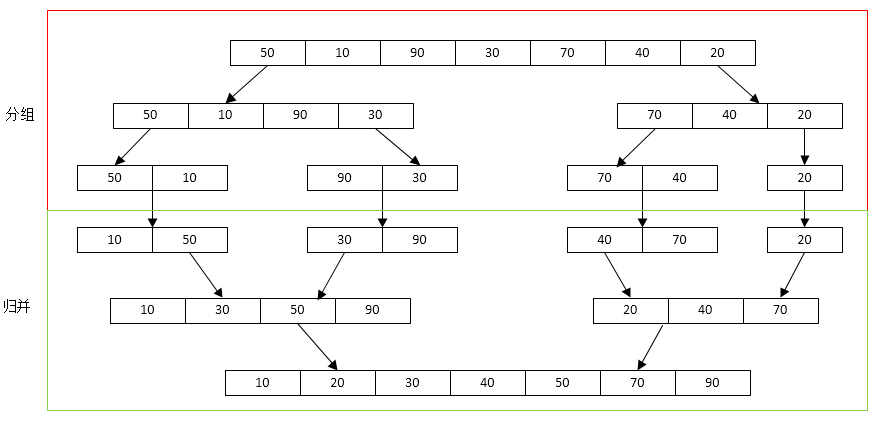
代码实例:
static void Main(string[] args){ int[] list = { 50, 10, 90, 30, 70, 40, 20 }; MeSort(list, 0, list.Length - 1); Console.WriteLine("归并排序的结果:{0}", string.Join(",", list));}static void MeSort(int[] list, int start, int end){ if (start < end) { int middle = (start + end) / 2; /*对数组进行分组*/ MeSort(list, start, middle); /*分组左序列*/ MeSort(list, middle + 1, end); /*分组右序列*/ MergeS(list, start, middle, end); /*对左右序列进行合并(归并)*/ }}static void MergeS(int[] list, int first, int middle, int end){ int IndexA = first; /*左序列起始位置*/ int IndexB = middle + 1; /*右序列起始位置*/ int[] tempList = new int[end - first + 1]; /*左右序列合并后的临时数组*/ int tempIndex = 0; while (IndexA <= middle && IndexB <= end) /*循环左右序列中的数据*/ { if (list[IndexA] >= list[IndexB]) /*对比左右序列中数据大小*/ { tempList[tempIndex++] = list[IndexB++]; /*右元素大于左元素,把右元素存放到临时数组tempList中,并把临时数组tempIndex++,然后在取右序列中下一元素*/ } else { tempList[tempIndex++] = list[IndexA++]; /*左元素大于右元素,把左元素存放到临时数组tempList中,并把临时数组tempIndex++,然后在取在序列中下一元素*/ } } while (IndexA <= middle) /*有一侧子表遍历完后,跳出循环,将另外一侧子表剩下的数一次放入暂存数组中*/ { tempList[tempIndex++] = list[IndexA++]; } while (IndexB <= end) { tempList[tempIndex++] = list[IndexB++]; } tempIndex = 0; /*设置临时数组从第1位开始替换*/ for (int i = first; i <= end; i++) /*临时数组替换List数组中数据*/ { list[i] = tempList[tempIndex++]; }}
快速排序(quick sort) |
排序思想:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
复杂度:O(nlogn) 。
稳定性:不稳定。

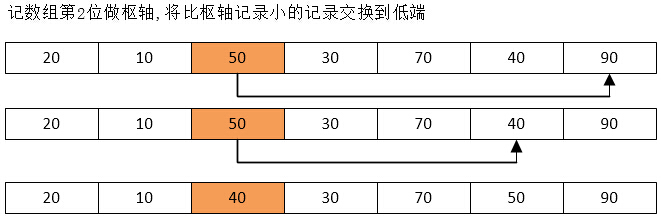
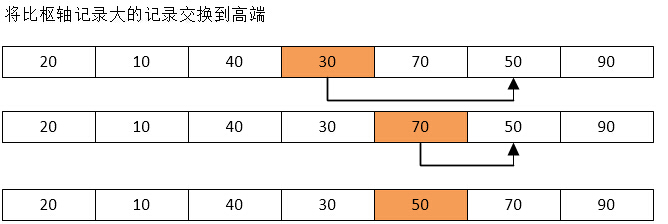


代码实例:
static void Main(string[] args) { int[] list = { 50, 10, 90, 30, 70, 40, 20 }; QuickSort(list, 0, list.Length - 1); Console.WriteLine("快速排序的结果:{0}", string.Join(",", list)); } private static void QuickSort(int[] list, int start, int end) { int pivot; if (start < end) { pivot = Partition(list, start, end); /* 对序列一分为二数出中间值 */ QuickSort(list, start, pivot - 1); /* 对低端序列进行排序 */ QuickSort(list, pivot + 1, end); /* 对高端序列进行排序 */ } } private static int Partition(int[] list, int first, int end) { int pivotkey = list[first]; /* 默认取序列中第0位为枢轴 */ while (first < end) { while (first < end && list[end] >= pivotkey) /*比枢轴小的记录交换到低端*/ { end--; } swap(list, first, end); while (first < end && list[first] <= pivotkey) /*比枢轴大的记录交换到高端*/ { first++; } swap(list, first, end); } return first; /*返回枢轴值*/ } /// <summary> /// 替换数组A于B之间的位置 /// </summary> private static void swap(int[] list, int A, int B) { int temp = list[A]; list[A] = list[B]; list[B] = temp; }
常见排序方法基本就这些。已分享完毕.....
排序性能和速度快速排序优于其他常见排序方法。